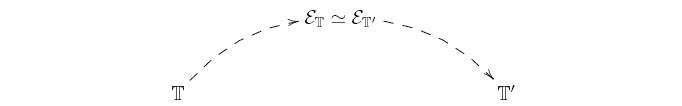The theory of topos-theoretic ‘bridges’: an introduction
The aim of this tutorial is to offer a gentle introduction to the
theory of topos-theoretic 'bridges', that is to the way in which
Grothendieck toposes can be used as unifying spaces connecting different
mathematical theories with each other and enabling an effective trasfer
of information between them.
Grothendieck toposes are mathematical objects which are built from a pair, called a
site, consisting of a category and a notion of 'covering'
of its objects by families of arrows, called a Grothendieck topology, in
a certain canonical way: by definition, a Grothendieck topos is any
category which is equivalent to the category of sheaves on a site. Very
importantly, different sites may give rise to equivalent toposes.
Thanks to the pioneeing work of the categorical logicians active in
the seventies, notably including Makkai and Reyes [4], to any mathematical theory (of a general specified form
- technically speaking a geometric theory) one can canonically associate a
Grothendieck topos, called its
classifying topos, which classifies its models (in
arbitrary Grothendieck toposes) and hence represents 'the' natural framework in which the theory should be investigated, both in itself and in relationship to other theories. Two theories having the same classifying toposes (up to equivalence) are said to be
Morita-equivalent. We can think of two
Morita-equivalent theories as two theories who express the same
mathematical content in different languages.
The existence of theories which are Morita-equivalent to each other
translates, at the level of sites, into the existence of different sites
generating the same topos (up to equivalence); indeed, to any theory
one
can canonically associate a site such that the topos of sheaves on it can
be identified with its classifying topos
.
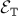The basic idea underlying the
'bridge' technique is that the classifying topos
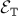of a
theory can be effectively used as a 'bridge' to transfer information between the theory
and any other theory
which is Morita-equivalent to it:
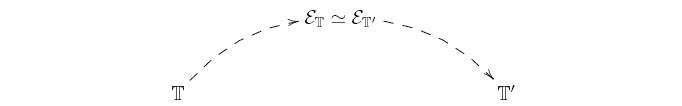
The transfer of knowledge between the two theories takes place
as follows. For any topos-theoretic invariant (i.e. property or construction of toposes which is
invariant under equivalence of toposes), one
tries to express it first in terms of one theory and then in terms of
the other; provided that one obtains appropriate characterizations
connecting properties of theories and properties of their classifying
toposes (equivalently, characterizations connecting properties of sites
and properties of toposes), this will lead to a logical relationship
between properties of the two theories written in their respective
languages.
The results arising from an application of this technique are often deep
and surprising, in that a given invariant can manifest itself in
significantly different ways in the context of different theories or
sites, giving rise to a veritable mathematical morphogenesis.
This view of toposes as 'bridges' was originally introduced in [1]
and has been further developed in [2]; a self-contained introduction is
provided by the author's habilitation thesis [3], which also contains a
selection of notable applications of this theory in different fields of
Mathematics obtained throughout the past years.
The tutorial will consist of three lectures:
(1) Theories. In this lecture I will
introduce geometric logic and its categorical semantics.
(2) Sites. In this lecture I will explain the
geometric approach to toposes through sites, by discussing the main
properties of categories of sheaves on a site.
(3) Toposes. In this lecture I will review
the theory of classifying toposes, the notion of Morita-equivalence and
describe
the way in which Grothendieck toposes can effectively serve as 'bridges'
between theories, by discussing examples pertaining to different fields
of Mathematics.
References:
[1] O. Caramello, The unification of Mathematics via
Topos Theory,
arXiv:math.CT/1006.3930 (2010).
[2] O. Caramello, Theories, Sites, Toposes: Relating and
studying mathematical theories through topos-theoretic 'bridges'
(Oxford University Press, forthcoming)
[3] O. Caramello, Grothendieck toposes as unifying
'bridges' in Mathematics,
habilitation thesis, University of Paris 7 (2016).
[4] M. Makkai and G. Reyes, First-Order
Categorical Logic, Lecture Notes in Math., vol. 611,
Springer-Verlag (1977).