Olivia Caramello's website
Unifying theory
A more technical explanation
Geometric theories and classifying toposes
The classifying topos of a
geometric theory
![]() (that is, of
a first-order theory whose axioms can be presented in the form
(that is, of
a first-order theory whose axioms can be presented in the form
![]() ,
where
,
where ![]() and
and
![]() are first-order
formulas obtained from atomic formulae by only using finitary
conjunctions, infinitary disjunctions and existential quantifications
and
are first-order
formulas obtained from atomic formulae by only using finitary
conjunctions, infinitary disjunctions and existential quantifications
and ![]() is a set of
variables containing all the free variables of
is a set of
variables containing all the free variables of
![]() and
and
![]() ) is a
Grothendieck topos
) is a
Grothendieck topos
![]() which classifies the models of
which classifies the models of
![]() in
Grothendieck toposes, in the sense that for any Grothendieck topos
in
Grothendieck toposes, in the sense that for any Grothendieck topos
![]() there is an
equivalence of categories
there is an
equivalence of categories
![]()
natural in
![]() , where
, where
![]() is the category of
geometric
morphisms from
is the category of
geometric
morphisms from ![]() to
to ![]() and
and
![]() is the category of models of the theory
is the category of models of the theory
![]() in the topos
in the topos
![]() . In other words,
there is a model
. In other words,
there is a model ![]() of
of
![]() in
in
![]() ,
called 'the' universal model of
,
called 'the' universal model of
![]() ,
characterized by the universal property that any model
,
characterized by the universal property that any model
![]() in a Grothendieck
topos
in a Grothendieck
topos ![]() can be
obtained, up to isomorphism, as a pullback
can be
obtained, up to isomorphism, as a pullback
![]() of the model
of the model
![]() along the inverse
image
along the inverse
image ![]() of
a unique (up to isomorphism) geometric morphism
of
a unique (up to isomorphism) geometric morphism
![]() from
from
![]() to
to
![]() , a
sort of 'shadow' of
, a
sort of 'shadow' of ![]() . In
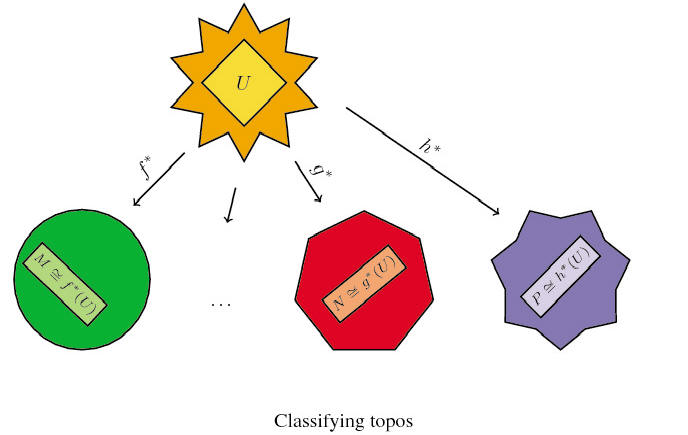
the following picture, the big shapes represent different toposes while
the inner lighter shapes represent models of a given theory inside them;
in particular, the dark yellow star represent the classifying topos of a
given
theory and the light yellow diamond
. In
the following picture, the big shapes represent different toposes while
the inner lighter shapes represent models of a given theory inside them;
in particular, the dark yellow star represent the classifying topos of a
given
theory and the light yellow diamond ![]() represent the universal model of the theory inside it.
represent the universal model of the theory inside it.
It is a fact that most of the (first-order) theories naturally
arising in Mathematics have a geometric axiomatization (over their
signature). Anyway, if a finitary first-order theory
![]() is not geometric, we can canonically construct a coherent theory over a larger signature, called the
Morleyization of
is not geometric, we can canonically construct a coherent theory over a larger signature, called the
Morleyization of
![]() , whose models in the category
Set of sets (and, more generally, in any Boolean coherent category) can be identified with those of
, whose models in the category
Set of sets (and, more generally, in any Boolean coherent category) can be identified with those of
![]() .
The notion of Morleyization is important because it enables us to study any kind of first-order theory by using the methods of Topos Theory. In fact, we can expect many important properties of first-order theories to be naturally expressible as properties of their Morleyizations, and these latter properties to be in turn expressible in terms of
invariant properties of their classifying toposes. For example, a
first-order theory
.
The notion of Morleyization is important because it enables us to study any kind of first-order theory by using the methods of Topos Theory. In fact, we can expect many important properties of first-order theories to be naturally expressible as properties of their Morleyizations, and these latter properties to be in turn expressible in terms of
invariant properties of their classifying toposes. For example, a
first-order theory
![]() is complete if and only if its Morleyization
is complete if and only if its Morleyization
![]() satisfies the following property: any coherent (equivalently, geometric)
sentence over its signature is provably equivalent to
satisfies the following property: any coherent (equivalently, geometric)
sentence over its signature is provably equivalent to
![]() or to
or to
![]() , but not both; and this property is precisely equivalent to saying that its classifying topos is two-valued.
, but not both; and this property is precisely equivalent to saying that its classifying topos is two-valued.
It is often the case that one can 'turn' a finitary first-order theory into a geometric one by adding some sorts to the signature of the original theory and axioms in the extended language so to ensure that each of the first-order formulae which appear in the axioms of the original theory becomes equivalent to geometric formulae in the extended signature. Notice that the Morleyization represents a canonical way for doing this which works for any kind of first-order theory, but that one can nonetheless, in particular cases, obtain a geometric theory starting from a finitary first-order one whose set-theoretic models can be identified with those of the original theory in alternative ways, as indicated above.
The classifying topos of a geometric theory can be canonically built as the category of sheaves on the geometric syntactic category of the theory with respect to the geometric topology on it. For smaller fragments of geometric logic, such as for example Horn (resp. regular, coherent) logic, there exist variations of this syntactic construction, consisting in replacing the geometric syntatic site of the theory with its cartesian (resp. regular, coherent) syntactic site. In particular, any finitary algebraic theory can be realized as the topos of presheaves on its cartesian syntactic category.
There are also methods of different nature for 'calculating' the classifying topos of a geometric theory. For example, as we shall see below, every representation of a geometric theory as an extension of a given geometric theory over its language leads to a representation of its classifying topos as a subtopos of the classifying topos of the latter theory. In fact, more generally, it is reasonable to expect 'different ways of looking at a certain theory' to materialize into different representations of its classifying topos (see the discussion below).
We said above that to any geometric theory one can associate a
site, namely the geometric syntatic site of the theory, such that its
classifying topos is equivalent to the category of sheaves on this site.
Conversely, every Grothendieck topos can be regarded, although not
canonically, as the classifying topos of a geometric theory; indeed, if a topos
![]() is represented as
the category of sheaves
is represented as
the category of sheaves
![]() on a site
on a site
![]() then
then
![]() can be regarded as
the classifying topos of the geometric theory of
can be regarded as
the classifying topos of the geometric theory of
![]() -continuous flat
functors on
-continuous flat
functors on ![]() .
.
The existence of Morita-equivalences between different theories can thus be interpreted geometrically as the existence of different sites of definition for a given topos. The representation theory for Grothendieck toposes in terms of sites therefore becomes an essential tool for investigating Morita-equivalences.
The 'bridge-building' technique
The unifying methodologies are based on the construction of topos-theoretic 'bridges' connecting distinct mathematical theories with each other.
If ![]() and
and
![]() are two
Morita-equivalent theories (that is, geometric theories
classified by the same topos) then their common classifying topos can be
used as a 'bridge' for transferring information between them:
are two
Morita-equivalent theories (that is, geometric theories
classified by the same topos) then their common classifying topos can be
used as a 'bridge' for transferring information between them:
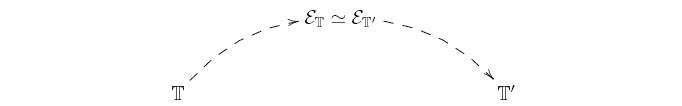
The transfer of information takes place by expressing topos-theoretic
invariants (that is, properties or constructions on
toposes which are stable under categorical equivalences) defined on their
common classifying topos directly in terms of the theories
![]() and
and
![]() . This is
done by associating to each of the two theories a site of definition for
its classifying topos (for example, its geometric syntactic site) and
then
using site characterizations (that is,
characterizations of topos-theoretic invariants on a topos
. This is
done by associating to each of the two theories a site of definition for
its classifying topos (for example, its geometric syntactic site) and
then
using site characterizations (that is,
characterizations of topos-theoretic invariants on a topos
![]() in terms of
its sites of definition, i.e. of the sites
in terms of
its sites of definition, i.e. of the sites
![]() such that
such that
![]() is
categorically equivalent to
is
categorically equivalent to
![]() ) to establish
relationships between the resulting sites.
) to establish
relationships between the resulting sites.
Specifically, suppose that
![]() and
and
![]() are two sites
of definition for the same topos, and that
are two sites
of definition for the same topos, and that
![]() is a topos-theoretic
invariant. Then one can seek site characterizations for the invariant
is a topos-theoretic
invariant. Then one can seek site characterizations for the invariant
![]() , that is (in the
case
, that is (in the
case ![]() is a property -
the case of
is a property -
the case of
![]() being a
'construction' admits an analogous treatment which we do not address in
full generality here)
a logical equivalence of the kind 'the topos
being a
'construction' admits an analogous treatment which we do not address in
full generality here)
a logical equivalence of the kind 'the topos
![]() satisfies
satisfies
![]() if and only if
if and only if
![]() satisfies a property
satisfies a property
![]() (written in
the language of the site
(written in
the language of the site
![]() )' and,
similarly for
)' and,
similarly for ![]() ,
a logical equivalence of the kind 'the topos
,
a logical equivalence of the kind 'the topos
![]() satisfies
satisfies
![]() if and only if
if and only if ![]() satisfies a property
satisfies a property
![]() '.
'.
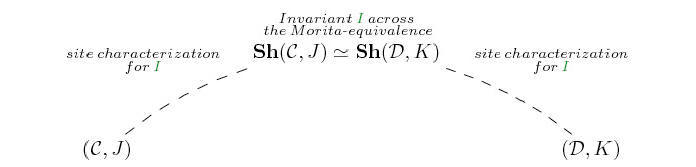
Clearly, such characterizations immediately
lead to a logical equivalence between the properties
![]() and
and
![]() of the two
sites, which can then be seen as different manifestations of a
unique property, namely
of the two
sites, which can then be seen as different manifestations of a
unique property, namely
![]() , in the context of
the two different sites
, in the context of
the two different sites
![]() and
and ![]() .
.
The crucial aspect here is that the 'bridge technique' allows to interpret and study a large part of dualities and equivalences arising in Mathematics through the investigation of the representation theory of Grothendieck toposes and the site-level characterization of topos-theoretic invariants. The theory of Grothendieck toposes and their representations thus becomes a sort of 'meta-theory of mathematical duality', which makes it possible to effectively compare distinct mathematical theories with each other and transfer knowledge between them.
In the following section we discuss more in detail the subject of Morita-equivalences, which play in our context the role of 'decks' of our 'bridges', and of site characterizations for topos-theoretic invariants, which constitute the 'arches' of our 'bridges'.
Decks of bridges: Morita-equivalences
Two geometric theories
![]() and
and
![]() are
Morita-equivalent if and only if they have equivalent categories of
models in every Grothendieck topos
are
Morita-equivalent if and only if they have equivalent categories of
models in every Grothendieck topos
![]() , naturally in
, naturally in
![]() , that is if for
each Grothendieck topos
, that is if for
each Grothendieck topos
![]() there is an
equivalence of categories
there is an
equivalence of categories
![]()
such that for any geometric morphism
![]() the following diagram commutes (up to isomorphism):
the following diagram commutes (up to isomorphism):

Of course, the
classifying topos being the representing object for the semantics
(pseudo)functor
![]() of
the theory
of
the theory
![]() , two theories
are Morita-equivalent if and only if they have the same classifying
topos (up to equivalence).
, two theories
are Morita-equivalent if and only if they have the same classifying
topos (up to equivalence).
Given the level of technical sophistication of this definition, it is reasonable to wonder if Morita-equivalences naturally arise in Mathematics and, in case, if there are systematic ways for 'generating' them. The following remarks are meant to show that the answer to both these questions is positive.
-
If two geometric theories
 and
and
 have
equivalent categories of models in the category Set
then, provided that the given categorical equivalence
have
equivalent categories of models in the category Set
then, provided that the given categorical equivalence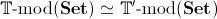
is established by using only constructive logic (that is, by avoiding for instance the law of excluded middle and the axiom of choice) and geometric constructions (that is, by only using set-theoretic constructions which involve finite limits and small colimits, equivalently which admit a syntactic formulation involving only equalities, finite conjunctions, (possibly) infinitary disjunctions and existential quantifications), it is reasonable to expect the original equivalence to 'lift' to a Morita-equivalence
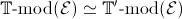
between
 and
and
 .
. -
Two cartesian (in particular, finitary algebraic) theories
 and
and
 have equivalent categories of models in
Set if and only if they are Morita-equivalent (or,
equivalently, if and only if their cartesian syntactic categories
are equivalent).
have equivalent categories of models in
Set if and only if they are Morita-equivalent (or,
equivalently, if and only if their cartesian syntactic categories
are equivalent).
[Indeed,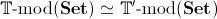 if and only if the cartesian syntactic categories of
if and only if the cartesian syntactic categories of
 and
and
 are
equivalent (since for any such theory its category of models in
Set is equivalent to the category of cartesian functors
from its syntactic category to Set), if and only if the classifying toposes of
are
equivalent (since for any such theory its category of models in
Set is equivalent to the category of cartesian functors
from its syntactic category to Set), if and only if the classifying toposes of
 and
and
 (which are equivalent respectively to the presheaf topos on the
cartesian syntactic category of
(which are equivalent respectively to the presheaf topos on the
cartesian syntactic category of
 and to
the presheaf topos on the cartesian syntactic category of
and to
the presheaf topos on the cartesian syntactic category of
 ) are
equivalent.]
) are
equivalent.] -
If two geometric (resp. coherent) theories have equivalent geometric (resp. coherent) syntactic categories then they are Morita-equivalent.
[Indeed, the classifying topos can be constructed as the category of sheaves on the syntactic site of the theory and the Grothendieck topologies on the syntactic sites can be defined intrinsically in terms of the categorical structures on the underlying categories.] -
If two finitary first-order theories are biinterpretable (in the sense of classical Model Theory) then their Morleyizations are Morita-equivalent.
[Indeed, the coherent syntactic category of the Morleyization of a first-order theory is equivalent to the first-order syntatic category of the theory.] -
Two associative rings with unit are Morita-equivalent (in the classical, ring-theoretic, sense) if and only if the algebraic theories axiomatizing the (left) modules over them are Morita-equivalent (in the topos-theoretic sense). In fact, two rings are Morita-equivalent if and only if the cartesian syntactic categories of these theories are equivalent.
[Indeed, by the first remark above, these theories are Morita-equivalent if and only if their categories of set-based models are equivalent (equivalent, if and only if their cartesian syntactic categories are equivalent), that is if and only if the categories of (left) modules over the two rings are equivalent. Specifically, for each ring R the theory axiomatizing its (left) R-modules can be defined as the theory obtained from the algebraic theory of abelian groups by adding one unary function symbol for each element of the ring and writing down the obvious axioms involving the terms formed with such symbols as well as with the symbol for addition in the group which express the conditions in the definition of R-module.] -
Other notions of Morita-equivalence for various kinds of algebraic or geometric structures considered in the literature can be reformulated as equivalences between different representations of the same topos, and hence as Morita-equivalences between different geometric theories. For instance:
- Two topological groups are Morita-equivalent (in the sense of this paper) if and only if the toposes of continuous actions over them are equivalent. (A natural analogue of this notion for topological and localic groupoids has been studied by several authors and a summary of the main results in contained in section C5.3 of this book).
- Two small categories are Morita-equivalent (in the sense of this paper) if and only if the corresponding presheaf toposes are equivalent, that is if and only if their Karoubian completions are equivalent.
- Two inverse semigroups are Morita-equivalent (in the sense of this paper or, equivalently, of this paper) if and only if their classifying toposes (as defined in this paper) are equivalent (cf. this paper). -
Categorical dualities or equivalences between 'concrete' categories can often be seen as arising from the process of 'functorializing' Morita-equivalences which express structural relationships between each pair of objects corresponding to each other under the given duality or equivalence (cf. for example this paper and this paper).
[In fact, the theory of geometric morphisms of toposes provides various natural ways of 'functorializing' bunches of Morita-equivalences.] -
As a matter of fact, the notion of Morita-equivalences materializes in many situations the intuitive feeling of 'looking at the same thing in different ways', meaning, for instance, describing the same structure(s) in different languages or constructing a given object in different ways.
[Concrete examples of this general remark can be found for instance in this paper, where the different constructions of the Zariski spectrum of a ring, of the Gelfand spectrum of a C*-algebra, and of the Stone-Cech compactification of a topological space are interpreted as Morita-equivalences between different theories.] -
Different ways of looking at a given mathematical theory can often be formalized as Morita-equivalences.
Indeed, different ways of describing the structures axiomatized by a given theory can often give rise to a theory written in a different language whose models (in any Grothendieck topos) can be identified, in a natural way, with those of the former theory and which is therefore Morita-equivalent to it. -
A geometric theory alone generates an infinite number of Morita-equivalences, via its 'internal dynamics'. In fact, any way of looking at a geometric theory as an exension of a geometric theory written in its signature provides a different representation of its classifying topos, as a subtopos of the classifying topos of the latter theory (cf. the duality theorem).
[An intuitive image which may help understand this remark is the following. We can think of a mathematical theory as a living organism which is born when its original axioms are given and which develops in time through the discovery of new results in it. Any collection of results which are already known to hold in the theory can be taken as axioms of a new theory of which the former theory can be viewed as an extension and hence leads, by the remark above, to a new representation of its classifying topos. Any splitting between the already known (say, the 'past' of the theory) and the potentially true (that is, the 'future' of the theory) thus gives rise to a Morita-equivalence of the theory with another one (via the duality theorem).] -
Different sites of definition for a given topos can be interpreted logically as Morita-equivalences between different theories (in fact, the converse also holds, in the sense that any Morita-equivalence gives canonically rise to two different sites of definition of the common classifying topos). The representation theory of Grothendieck toposes in terms of sites (and, more generally, any technique that one may employ for obtaining a different site of definition for a given topos) thus constitutes an effective tool for generating Morita-equivalences. For example, (a version of) Grothendieck's Comparison Lemma asserts that for any site
 and any
full subcategory
and any
full subcategory  of
of 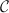 which
is
which
is 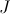 -dense (that
is, for every object of
-dense (that
is, for every object of 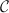 there
exists a
there
exists a 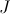 -covering
sieve on it generated by arrows whose domains lie in
-covering
sieve on it generated by arrows whose domains lie in
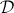 ), we have an
equivalence
), we have an
equivalence
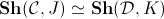 ,
where
,
where  is the
Grothendieck topology on
is the
Grothendieck topology on
 induced by
induced by
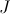 .
. -
Different separating sets for a given topos (recall that a separating set for a topos is a set of objects of the topos such that any object in the topos can be covered by a family of arrows whose domains belong to the set) give rise to different sites of definition for it; indeed, for any separating set of objects
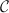 of a
Grothendieck topos
of a
Grothendieck topos
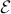 , we have an
equivalence
, we have an
equivalence
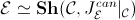 , where
, where
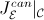 is the
Grothendieck topology on
is the
Grothendieck topology on
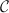 induced
by the canonical topology on
induced
by the canonical topology on
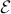 . Notice
incidentally that all the sites of the form
. Notice
incidentally that all the sites of the form
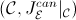 are
subcanonical, and any subcanonical site of definition for the topos
are
subcanonical, and any subcanonical site of definition for the topos
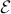 is, up to
canonical equivalence, of this form. In
particular, for any topological space
is, up to
canonical equivalence, of this form. In
particular, for any topological space 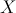 and any basis
and any basis
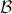 for it,
we have an equivalence
for it,
we have an equivalence
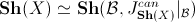 (as we
shall see in this section and
this other one, the most interesting
Morita-equivalences arise when the topology
(as we
shall see in this section and
this other one, the most interesting
Morita-equivalences arise when the topology
 can be
characterized intrinsically in terms of
can be
characterized intrinsically in terms of
 ).
).
[Indeed, a Grothendieck topos behaves logically as a 'generalized
universe of sets' in which one can perform most of the classical
set-theoretic constructions with the only significant exception of
arguments requiring non-constructive principles, and hence we can
naturally expect to be able to generalize the original equivalence
between the categories of set-based models of the two theories to
the case of models in arbitrary Grothendieck topos; and the fact
that the constructions involved in the definition of the equivalence
are geometric ensures that the naturality condition for
Morita-equivalences mentioned above is satisfied (since geometric
constructions are preserved by inverse image functors of geometric
morphisms, so that one can
globally obtains a Morita-equivalence.
See Exercises VIII.7-8-9 in
this book for an example of application of this general method
to the case of the equivalence between the category of models of the
theory of decidable (resp. infinite decidable) objects and the
theory of flat (resp. flat and continuous with respect to the atomic
topology) functors on the opposite of the category of finite sets
and injections between them. A more general investigation of of this
method in the context of theories of presheaf type is pursued in
this paper, leading to a criterion for a geometric theory to be
of presheaf type which is applicable to a wide class of theories
whose finitely presentable models are finite.]
Arches of bridges: site characterizations
As we remarked above, the bridge technique is based on the existence of site characterizations for topos-theoretic invariants, that is criteria connecting invariant properties (resp. constructions) on toposes and properties (resp. constructions) of their sites of definition (written in their respective languages).
It thus becomes crucial to investigate the behaviour of topos-theoretic invariants with respect to sites. As a matter of fact, such a behaviour is often very natural, in the sense that topos-theoretic invariants of whatever kind generally admit natural site characterizations, which explains the technical effectiveness of the 'bridge method'.
For instance, bijective characterizations for a wide class of geometric invariants of toposes, notably including the property of a topos to be atomic (resp. locally connected, localic, equivalent to a presheaf topos, compact, two-valued) were obtained in this paper.
Also, several notable invariants of subtoposes were shown in this paper to admit natural site chacterizations as well as explicit logical descriptions in terms of the theories classified by the relevant toposes.
Moreover, it was shown in this paper that a wide class of logically-inspired invariants of topos, obtained by interpreting first-order formulae written in the language of Heyting algebras, admit natural and bijective site characterizations.
Topos-theoretic invariants relevant in Algebraic Geometry and Homotopy Theory, such as for example the cohomology and homotopy groups of toposes, are also well-known to admit, at least in many important cases, natural characterizations in terms of sites.
The startling aspect in all of this is that, while it is often possible to obtain, by using topos-theoretic methods, site characterizations for topos-theoretic invariants holding for wide classes of sites, such criteria can be highly non-trivial as far as their mathematical depth is concerned (since the representation theory of toposes is by all means a non-trivial subject) and hence, when applied to specific Morita-equivalences, can lead to deep results on the relevant theories (especially when the given Morita-equivalence is a non-trivial one).
In fact, these insights can be very surprising, when observed from a
concrete point of view (that is, from the point of view of the two sites
related by the Morita-equivalence), since a given topos-theoretic
invariant may manifest itself in very different ways in the context of
different sites. For example, for any site
![]() the topos
the topos
![]() satisfies the
invariant property to be De Morgan if and only if for any object
satisfies the
invariant property to be De Morgan if and only if for any object
![]() of the
category
of the
category ![]() and any
and any
![]() -closed sieve
-closed sieve
![]() on
on
![]() the sieve
the sieve
![]()
is ![]() -covering,
where
-covering,
where ![]() (for any
(for any
![]() ).
).
In particular, such property specializes, on a presheaf topos, to the condition on the underlying category to satisfy the dual of the amalgamation property (that is, the property that any two pairs of arrows with common codomain can be completed to a commutative square), while on a topos of sheaves on a topological space it specializes to the property of the space to be estremally disconnected. Further examples of the behavior of topos-theoretic invariants with respect to sites are provided in this section.
In light of these results, it is reasonable to expect that many more topos-theoretic invariants that one might introduce will admit natural site characterizations; in fact, one of the purposes of the unification programme is to document the behaviour of topos-theoretic invariants in relation to sites and develop general methods for obtaining site characterizations for new as well as known invariants.
Notice that the unifying method based on the view 'toposes as bridges' generates results transverally to the various mathematical fields, in a uniform and effective way which is determined by the form of the toposes involved and the invariants considered on them.
It is worth to remark that, unlike the traditional, 'dictionary-oriented' method of translation based on a 'renaming', according to the given 'dictionary', of the primitive constituents of the information across the two different languages, our 'invariant-oriented' method of translation of results across different mathematical theories based on topos-theoretic bridges proceeds through a 'structural unraveling' of appropriate invariants across different representations of the toposes involved, rather than through the use of an explicit description of the Morita-equivalence serving as 'dictionary'. In fact, for the transfer of 'global' properties of toposes, it is only the existence of a Morita-equivalence that really matters, and we can well ignore its actual definition (since, by definition, a topos-theoretic invariant is stable under any kind of categorical equivalence); of course, if one wants to establish more 'specific' results, an explicit description of the Morita-equivalence becomes necessary (in which case, one can use invariant properties of objects of toposes rather than invariants properties of the 'whole topos') but for treating most of the 'global' properties of theories this is not at all necessary.
We should also remark that the arches of a given bridges need not necessarily be 'symmetric', that is arising from the instantiation in the context of two given sites of a unique site characterization holding for both of them. Indeed, for any given Morita-equivalence and topos-theoretic invariant, the invariant can admit a certain site characterizations holding for sites of a given form including one of the sites involved in the Morita-equivalence but not the other, which constitute one of the arches of the bridge, and another site characterization holding in particular for the other site, yielding the other arc of the bridge. As an example, take the property of a topos to be coherent: this property does not admit an 'elementary' bijective site characterization holding for all sites, but it admits a bijective site characterization holding for all trivial sites (i.e. sites in which the Grothendieck topology is trivial) and an implicative characterization of the kind 'if a theory is coherent, then its classifying topos is coherent', which can be combined together to obtain a bridge expressing a theorem about theories of presheaf type.
As an illustration of the natural behaviour of topos-theoretic invariants with respect to sites and geometric theories, we focus in the next section on the notion of subtopos.
The duality theorem
The notion of
subtopos is a topos-theoretic invariant which has a natural
behaviour with respect to sites. Indeed, by a fundamental result in
Topos Theory, for any site
![]() the subtoposes
of a Grothendieck topos
the subtoposes
of a Grothendieck topos
![]() are in
bijective correspondence with the Grothendieck topologies on
are in
bijective correspondence with the Grothendieck topologies on
![]() which contain
which contain
![]() . Considered on the
classifying topos of a geometric theory, this characterization leads to
a description of these subtoposes as classifying toposes for theories
which extend the given theory over its signature.
. Considered on the
classifying topos of a geometric theory, this characterization leads to
a description of these subtoposes as classifying toposes for theories
which extend the given theory over its signature.
Specifically, given a geometric theory
![]() over a
signature
over a
signature ![]() , we
say that a geometric theory
, we
say that a geometric theory ![]() over
over
![]() is a
quotient of
is a
quotient of
![]() if every
geometric sequent over
if every
geometric sequent over
![]() which is
provable in
which is
provable in ![]() is provable in
is provable in ![]() (we shall consider quotients up to the equivalence relation which
identifies two quotients when they prove exactly the same geometric
sequents over their signature). Then we have the following duality
theorem (Theorem 3.6 in this
paper).
(we shall consider quotients up to the equivalence relation which
identifies two quotients when they prove exactly the same geometric
sequents over their signature). Then we have the following duality
theorem (Theorem 3.6 in this
paper).
Theorem: For any geometric theory
![]() , the
subtoposes of its classifying topos are in natural bijection
with the quotients of
, the
subtoposes of its classifying topos are in natural bijection
with the quotients of
![]() . Moreover,
under this assignment, any quotient of
. Moreover,
under this assignment, any quotient of ![]() corresponds
to its classifying topos.
corresponds
to its classifying topos.
Notice that this result can be interpreted as a site characterization for the property of being a subtopos on a given classifying topos in terms of the geometric syntactic site of a theory classified by it.
As shown in this paper, the theorem allows to transfer a lot of information known in Topos Theory about subtoposes into Logic; for instance, the collection of all subtoposes of a given topos is known to have the structure of a coHeyting algebra, (with the natural ordering on them), a structure which can be transferred at the level of sites and of theories (in the latter case across the bijection provided by the theorem). In fact, the lattice operations on Grothendieck topologies admit explicit and natural descriptions which can be used, among the other things, to obtain a logical characterizations of the Heyting algebra structure present on the collection of all the quotients of a given geometric theory.
The following picture is meant to represent the lattice structure on
the collection of subtoposes of a given topos
![]() and the isomorphic
structures (via the duality theorem) on the collection of quotients of
different theories (
and the isomorphic
structures (via the duality theorem) on the collection of quotients of
different theories (![]() ,
,
![]() ,
,
![]() , ...) classified by
, ...) classified by
![]() .
.
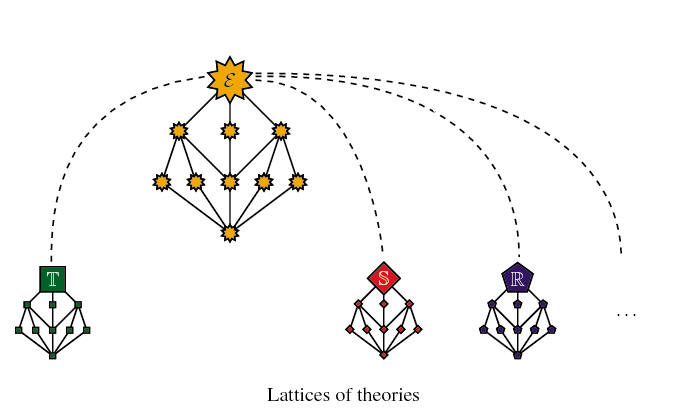
A truly remarkable fact is that the abstract topos-theoretic notions defined at the level of subtoposes, once transferred to the level of theories via the duality theorem, are often of very natural logical or mathematical interest.
For example, the subtopos arising as the surjection-inclusion
factorization of the geometric morphism ![]() to the classifying topos of a theory
to the classifying topos of a theory ![]() corresponding to a model
corresponding to a model
![]() of
of ![]() in
in ![]() can be
characterized as the classifying topos of the quotient of
can be
characterized as the classifying topos of the quotient of ![]() consisting of all the geometric sequents over the signature of
consisting of all the geometric sequents over the signature of ![]() which hold in the model
which hold in the model
![]() .
.
Another example is given by the notion of DeMorganization (resp. Booleanization) of a subtopos (as defined in this paper), whose logical interpretation defines a natural operation on theories. For instance, as shown in this paper, the DeMorganization of the (coherent) theory of fields can be identified with the theory of fields of finite characteristic which are algebraic over their prime fields, while its Booleanization can be identified with the theory of fields of finite characteristic which are algebraic over their prime fields as well as algebraically closed.
Let us now discuss the duality theorem in the context of the 'bridge-building' technique.
If we take two Morita-equivalent theories and associate to them their geometric syntactic sites then the syntactic characterizations given by the duality theorem yield a 'bridge' providing a bijection between the quotients of the two theories (written over their respective signatures). This result is interesting because, when specialized to concrete theories, it can be rather deep, and because it represents an instance of the unification between semantics (which is the context in which Morita-equivalences arise) and syntax (which is the context in which quotients lie) given by the theory of classifying toposes. Indeed, while in the setting of classical model theory one does not have, for general first-order theories, models of syntactic nature which enjoy a strong form of completeness, with the consequence that the semantics remain separate from the syntax and hence that it is not guaranteed that semantic equivalences of theories restrict to semantic equivalences for quotients of them (so that problems of the kind mentioned above are generally rather hard to approach), in the topos-theoretic context the universal models lying in classifying toposes satisfy a strong form of completeness, by virtue of the fact that they admit a purely syntactic description.
Another interesting context for the application of the duality
theorem in connection to the philosophy 'toposes as bridges' is given by
the class of theories of presheaf type. A geometric
theory is said to be of presheaf type if it is classified by a presheaf
topos. One can prove (see this
paper) that a theory ![]() is of presheaf type if and only if it is classified by the topos
is of presheaf type if and only if it is classified by the topos
![]()
where ![]() is
(a skeleton of) the category of finitely presentable models (that is,
the models such that their covariant hom-functor preserves filtered
colimits).
is
(a skeleton of) the category of finitely presentable models (that is,
the models such that their covariant hom-functor preserves filtered
colimits).
For any theory of presheaf type ![]() we thus have a Morita-equivalence
we thus have a Morita-equivalence
![]()
where ![]() is the geometric syntactic site of the theory
is the geometric syntactic site of the theory ![]() .
.
Considering the notion of subtopos as an invariant, and recalling the
site characterizations for this invariant obtained above (and in
particular the duality theorem), we obtain a 'bridge' between the two
different sites of definition yielding a bijection between the quotients
of the theory ![]() and the Grothendieck topologies on the opposite of the category
and the Grothendieck topologies on the opposite of the category ![]() .
For each quotient
.
For each quotient
![]() of
of ![]() we thus have a (unique) Grothendieck topology
we thus have a (unique) Grothendieck topology
![]() on
on
![]() such that the
given equivalence restricts (along the obvious geometric inclusions) to
an equivalence
such that the
given equivalence restricts (along the obvious geometric inclusions) to
an equivalence
![]()
Notice that the topology
![]() depends not only on
the quotient
depends not only on
the quotient
![]() but also
on the original equivalence of toposes
but also
on the original equivalence of toposes
![]()
since the composite of a geometric inclusion to a certain topos with an
equivalence on that topos is in general non-isomorphic to the original inclusion. Nonetheless, for each theory of presheaf type ![]() ,
one can always put an equivalence
,
one can always put an equivalence
![]()
in a canonical form, and hence explicitly describe the
relationship between the quotients
![]() and
their associated topologies
and
their associated topologies
![]() ; specifically, one
can suppose, without loss of generality, that for any theory of presheaf
type
; specifically, one
can suppose, without loss of generality, that for any theory of presheaf
type ![]() ,
the equivalence
,
the equivalence
![]()
is induced by the universal property of
![]() as a classifying applied to the model of
as a classifying applied to the model of ![]() in
in ![]() given by the
forgetful functor from
given by the
forgetful functor from
![]() to Set
(cf. this paper
for more details). We shall say that the given Morita-equivalence for
to Set
(cf. this paper
for more details). We shall say that the given Morita-equivalence for ![]() is canonical if it is of this form.
is canonical if it is of this form.
Any topos-theoretic invariant considered on a Morita-equivalence
![]()
thus gives rise, together with its site characterizations, to a 'bridge'

between the two different representations of the classifying topos.
An example of the insights which can be obtained by applying this
method, we have the following theorem, which exhibits relations
between 'geometric' properties of the site
![]() and
logical properties of the theory
and
logical properties of the theory
![]() . Of
course, each topos-theoretic invariant gives rise to a different
relation, and one can establish new relations by applying the same
general method to other topos-theoretic invariants. The
invariants which give rise to the following theorem are the property of
a topos to be equivalent to a presheaf topos (resp. to be atomic, to be
locally connected) and the property of an object of a topos to be
irreducible (resp. an atom, indecomposable), and the site
characterizations for them which are employed to derive the results are
provided by this paper.
. Of
course, each topos-theoretic invariant gives rise to a different
relation, and one can establish new relations by applying the same
general method to other topos-theoretic invariants. The
invariants which give rise to the following theorem are the property of
a topos to be equivalent to a presheaf topos (resp. to be atomic, to be
locally connected) and the property of an object of a topos to be
irreducible (resp. an atom, indecomposable), and the site
characterizations for them which are employed to derive the results are
provided by this paper.
Theorem. Let
![]() be a
quotient of a theory of presheaf type
be a
quotient of a theory of presheaf type
![]() over a
signature
over a
signature ![]() corresponding
to a Grothendieck topology
corresponding
to a Grothendieck topology ![]() on
on
![]() . Then
. Then
-
If
 is trivial then
is trivial then
 satisfies the property that there exists a collection
satisfies the property that there exists a collection
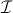 of
of
 -irreducible
geometric formulae-in-context over
-irreducible
geometric formulae-in-context over 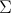 such that
for any geometric formula
such that
for any geometric formula
 over
over
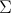 , there
exist formulae
, there
exist formulae 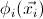 in
in
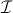 (for
(for 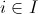 ) and
) and
 -provably
functional geometric formulae
-provably
functional geometric formulae
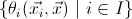 from the
from the 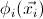 to
to
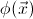 such that
such that
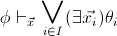 is provable in
is provable in
 (where by
(where by  -irreducible
formula we mean a geometric formula
-irreducible
formula we mean a geometric formula
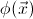 such that
for any family
such that
for any family
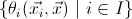 of
of
 -provably
functional geometric formulae from
-provably
functional geometric formulae from
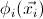 to
to
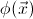 with the
property that
with the
property that
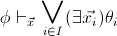 is provable in
is provable in
 ,
there exist
,
there exist 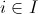 and a
and a  -provably
functional geometric formula
-provably
functional geometric formula
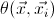 from
from
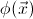 to
to
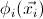 such that
such that
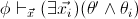 is provable in
is provable in
 ).
).
Moreover, if the Morita-equivalence for is canonical then every formula which presents a
is canonical then every formula which presents a
 -model is
-model is
 -irreducible.
-irreducible.
-
If the category
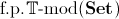 satisfies
the amalgamation property and
satisfies
the amalgamation property and
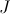 is the atomic
topology on the opposite of it then
is the atomic
topology on the opposite of it then
 satisfies the property that every geometric formula over its
signature is
satisfies the property that every geometric formula over its
signature is
 -provably
equivalent to a disjunction of
-provably
equivalent to a disjunction of
 -complete
formulae in the same context (where by a
-complete
formulae in the same context (where by a
 -complete
formula we mean a geometric formula
-complete
formula we mean a geometric formula
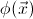 such that
the sequent
such that
the sequent
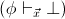 is
not provable in
is
not provable in
 and
for every geometric formula
and
for every geometric formula
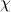 in the same
context either
in the same
context either
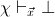 or
or
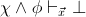 is
provable in
is
provable in
 ).
).
Moreover, if the Morita-equivalence for is canonical then every formula which presents a
is canonical then every formula which presents a
 -model is
-model is
 -complete.
-complete.
-
If the site
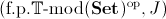 is
locally connected (that is, every
is
locally connected (that is, every
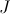 -covering sieve
is connected as a subcategory of the corresponding slice category)
then
-covering sieve
is connected as a subcategory of the corresponding slice category)
then  satisfies the property that if for any geometric formula
satisfies the property that if for any geometric formula
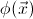 over
over
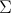 there
exists a (unique) family
there
exists a (unique) family
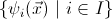 of
of
 --indecomposable
geometric formulae in the same context such that
--indecomposable
geometric formulae in the same context such that
for each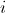 ,
,
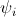
 -provably
implies
-provably
implies 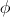 ,,
,,
for any distinct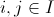 ,
,
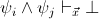 is provable in
is provable in
 ,, and
,, and
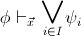 is provable in
is provable in

(where by a -indecomposable
geometric formula we mean a formula
-indecomposable
geometric formula we mean a formula
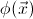 such that
for any family
such that
for any family
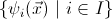 of
geometric formulae in the same context such that for each
of
geometric formulae in the same context such that for each
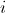 ,
, 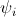
 -provably
implies
-provably
implies 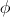 and
for any distinct
and
for any distinct
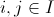 ,
,
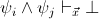 is provable in
is provable in
 , we
have that
, we
have that
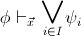 provable in
provable in
 implies
implies
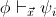 p
provable in
p
provable in
 for
some
for
some 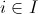 ).
).
Moreover, if the Morita-equivalence for is canonical then every formula which presents a
is canonical then every formula which presents a
 -model is
-model is
 -indecomposable.
-indecomposable.
This theorem might seem at first sight rather abstract and remote from the usual 'mathematical practice', but in fact concrete (and non-trivial) results about specific theories can be easily derived from it. For example, the theory of linear orders, as well as the theory of fields of finite characteristic which are algebraic over their prime fields, satisfy the first condition in the statement of the theorem, while the theory of atomless Boolean algebras, of infinite decidable objects, and of dense linear orders without endpoints satisfy the second condition. Please see this paper and this paper for more details.
Further concrete applications of the 'bridge method' are given in this section.
Finally, we show that it is possible to establish, under the hypothesis that the Morita-equivalence
![]()
for the theory ![]() be canonical, a precise description of the relation between the
quotients
be canonical, a precise description of the relation between the
quotients
![]() of
of ![]() and the Grothendieck topologies
and the Grothendieck topologies ![]() on
on
![]() corresponding
to them via the method above. Specifically, one can characterize the
models of
corresponding
to them via the method above. Specifically, one can characterize the
models of
![]() in
Grothendieck toposes among the models of
in
Grothendieck toposes among the models of ![]() directly in terms of the Grothendieck topology
directly in terms of the Grothendieck topology ![]() through a categorical, semantic, condition, and describe an
axiomatization of the theory
through a categorical, semantic, condition, and describe an
axiomatization of the theory
![]() directly in terms of
directly in terms of ![]() and
and ![]() .
.
As shown in this paper, in
any Grothendieck topos the
![]() -models
coincide with the
-models
coincide with the ![]() -models
which are
-models
which are ![]() -homogeneous
(in the sense of that paper). In particular, the models of
-homogeneous
(in the sense of that paper). In particular, the models of
![]() in
Set are precisely the models
in
Set are precisely the models
![]() of
of ![]() in Set such that for any finitely presentable
in Set such that for any finitely presentable ![]() -model
-model
![]() , any sieve
, any sieve
![]() and any
arrow
and any
arrow ![]() in
in
![]() there
exist an arrow
there
exist an arrow ![]() in
in ![]() and an arrow
and an arrow
![]() in
in
![]() such that
such that
![]() :
:

In particular, if the category
![]() satisfies the
amalgamation property (that is, the property that any pair of arrows
with common domain can be completed to a commutative square) then one
can consider the atomic topology
satisfies the
amalgamation property (that is, the property that any pair of arrows
with common domain can be completed to a commutative square) then one
can consider the atomic topology ![]() on it (that is, the Grothendieck topology on it such that its covering
sieves are precisely the non-empty ones), and the notion of
on it (that is, the Grothendieck topology on it such that its covering
sieves are precisely the non-empty ones), and the notion of ![]() -homogeneous
model specializes to that of homogeneous model, that is
of model
-homogeneous
model specializes to that of homogeneous model, that is
of model ![]() of
of ![]() in Set such that for any arrow
in Set such that for any arrow
![]() in
in
![]() and any
arrow
and any
arrow ![]() in
in
![]() there exists an
arrow
there exists an
arrow ![]() in
in
![]() such that
such that
![]() .
An illuminating application of the 'bridge technique' in connection to
the notion of homogeneous model is described in
this section.
.
An illuminating application of the 'bridge technique' in connection to
the notion of homogeneous model is described in
this section.
To obtain an explicit axiomatization of the quotient
![]() in
terms of
in
terms of ![]() , we
exploit the fact, established in
this
section, that the finitely presentable models of
, we
exploit the fact, established in
this
section, that the finitely presentable models of
![]() correspond to the
correspond to the ![]() -irreducible
formulae. From this it follows, in light of the duality theorem, that
-irreducible
formulae. From this it follows, in light of the duality theorem, that
![]() is
equal to the quotient
is
equal to the quotient
![]() of
of ![]() axiomatized by the sequents of the form
axiomatized by the sequents of the form
![]() ,
where
,
where ![]() and
and
![]() are
are
![]() -irreducible
formulae and
-irreducible
formulae and
![]() is a family of
is a family of
![]() -provably
functional geometric formulae from
-provably
functional geometric formulae from
![]() to
to
![]() with the
property that, regarded as a sieve on
with the
property that, regarded as a sieve on
![]() in
in
![]() ,
it is sent by the equivalence
,
it is sent by the equivalence
![]() to a
to a ![]() -covering
sieve on
-covering
sieve on ![]() .
.
The above-mentioned explicit construction of classifying toposes of quotients of theories of presheaf type via the the duality theorem can be regarded as a 'semantic' approach to the contruction of classifying toposes (as opposed to the syntactic approach consisting on taking the topos of sheaves on an appropriate syntactic site for the theory), which is particularly amenable for the applications in 'concrete' mathematical domains other than logic.
For example, by using this method one can calculate the classifying
topos for the theory of local rings (namely, the
Zariski topos) and the classifying topos for the
theory of integral domains, both regarded as quotient
of the theory of commutative rings with unit (which is of
presheaf type
being algebraic). Specifically, the classifying topos for the theory of
commutative rings with unit, axiomatized in the natural way over the
one-sorted the signature consisting of two binary function symbols
![]() and
and
![]() , one
unary function symbol
, one
unary function symbol
![]() and two
constants
and two
constants ![]() and
and
![]() , is the presheaf
topos
, is the presheaf
topos
![]() ,
where
,
where
![]() is the category of finitely generated (equivalently, finitely presented)
rings and ring homomorphisms between them. The theory of local rings can
be axiomatized as the quotient of this theory obtained by adding the
axioms
is the category of finitely generated (equivalently, finitely presented)
rings and ring homomorphisms between them. The theory of local rings can
be axiomatized as the quotient of this theory obtained by adding the
axioms
![]()
and
![]() ,
,
while the theory of integral domains is the quotient obtained by adding the axioms
![]()
and
![]() .
.
The classifying topos for the theory of local rings can be
represented as the topos
![]() ,
where
,
where ![]() is the
Grothendieck topology on
is the
Grothendieck topology on
![]() defined as follows: given a cosieve
defined as follows: given a cosieve
![]() in
in
![]() on an object
on an object ![]() ,
,
![]() if and
only if
if and
only if ![]() contains a
finite family
contains a
finite family
![]() of
canonical inclusions
of
canonical inclusions
![]() in
in
![]() where
where ![]() is any set of elements of
is any set of elements of
![]() which is not
contained in any proper ideal of
which is not
contained in any proper ideal of
![]() .
.
On the other hand, the classifying topos for the theory of integral
domains can be represented as the topos
![]() ,
where
,
where ![]() is
the Grothendieck topology on
is
the Grothendieck topology on
![]() defined as follows: given a cosieve
defined as follows: given a cosieve
![]() in
in
![]() on an object
on an object ![]() ,
,
![]() if
and only if either
if
and only if either ![]() is the zero ring and
is the zero ring and ![]() is the empty sieve on it
is the empty sieve on it
![]() contains a
non-empty finite family
contains a
non-empty finite family
![]() of
canonical projections
of
canonical projections
![]() in
in
![]() where
where ![]() is any set of elements of
is any set of elements of
![]() such that
such that
![]() .
.
Notice how the form of the two Grothendiek topologies
![]() and
and
![]() on the
category
on the
category
![]() reflects the form of the axioms of the two theories.
reflects the form of the axioms of the two theories.