Olivia Caramello's website
Unifying theory
Metaphors and analogies
T
An analogy with Astronomy: the 'classifying star' of a planet
An analogy with Linguistics: 'bridges' for translating
An analogy with Genetics: the classifying topos as a sort of DNA
Toposes as 'natural environments' for mathematical theories
Photographs from a plane: the importance of a
natural point of view
Reality as a unifying concept: 'bridges' between perceptions
Bridges in Finance: trading through stock
'bridging'
An analogy with Astronomy: the 'classifying star' of a planet
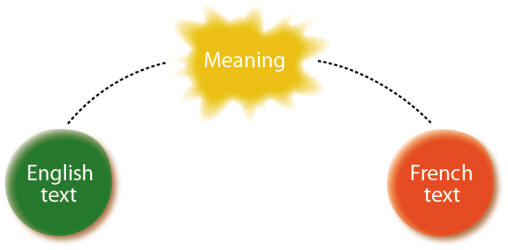
An analogy with Linguistics: 'bridges' for translating
The 'bridge-building' method for transferring information between two distinct mathematical theories can be interpreted as a method for translating information from the language of one theory into the language of the other theory. As such, it can be compared, at least conceptually, with the approaches developed in Linguisics for translating texts from one language into another.
A fundamental feature of a translation is the set of abstract properties of texts (for example, the meaning, the 'musicality', 'structural' features etc.) which it leaves invariant.
A literal translation proceeds in a bottom-up or dictionary-oriented way, as it consists, broadly speaking, in splitting the given text into sentences and then into words or short expressions, replacing each word (resp. short expression) in the first language with a word (resp. short expression) written in the other language which corresponds to it according to a given dictionary, and then assembling these words together 'from the bottom up' following possibly the same, or at most a similar, grammatical structure to that with which the corresponding original words were arranged in the text. From this description, it is clear that what is preserved by this kind of translation is the syntactical structure of the sentences which compose the texts, but not necessarily the meaning or musicality of the texts, which is what one would naturally expect from a good translation. This is why automatic or literal translations are often rather unsatisfactory, especially when they occur between languages which have radically different syntactical ways for expressing a given meaning.
This naturally raises the following question: which kind of approach should one adopt to obtain a good translation? Unlike a literal translation, a good translation should proceed in a top-down or invariant-oriented way, starting with the identification of a set of abstract properties of texts which one would like to remain invariant under the translation and then using any such property P (or the 'intersection' of all such properties) as a 'bridge' for translating between the two languages, as follows. Notice that for any such property P and any expression e in a given text, one can consider the 'value' Pe of the property P in the context of the expression e. Now, any given sentence e written in the first language, one computes the value Pe of P corresponding to it and then looks for the most appropriate sentence or syntactical expression e' in the second language whose value Pe' of the property P coincides with Pe. Note that in a translation of this kind it is not necessarily the syntactical structure to be preserved, as in the case of a literal translation, but the properties which are fixed at the beginning as the desired ones to remain invariant.
While a literal translation is neither particularly interesting nor deep conceptually, in that it essentially consists in a re-naming or re-labelling of the primitive constituents of a text according to a dictionary, a good, literary, translation is often a work of art, which can reveal new aspects of a text which were, in a sense, 'hidden' in the original version, allowing new and different interpretations of the message contained in it.
From a practical viewpoint, literal translations are essentially trivial and in fact they can, more or less easily, be mechanized, while good translations are much less canonical, and usually require some human imput, the ultimate reason for this being the fact that the properties which act as 'bridges' between the two languages are abstract and hence much harder to formalize, also in relation to their different expressions in the two languages, than a mere set of entries of a dictionary.
Let us now consider the analogues of these linguistic concepts in Mathematics. The mathematical analogue of natural languages are mathematical theories written in formal languages (in fact, one can think of a theory as a set of rules for arranging and manipulating the terms of a certain formal language, similarly to what happens in Linguistics where a grammar for a natural language defines the set of acceptable operations to be performed with the terms of the language).
Between two theories in Mathematics which share a common semantics, that is which represent different ways of talking about the same structures, one can attempt a translation of concepts and results written in their respective languages. As in Linguistics, this can be done by following a dictionary-oriented approach, that is by using an explicit 'translation function' (usually a bijection or equivalence of some sort, playing the role of the 'dictionary' - in fact, the notion of biinterpretability in Model Theory provides a good formalization of this idea) which sends primitive concepts in the language of the first theory to concepts expressed in the language of the other theory, or by following an invariant-oriented approach, based on the existence of a 'bridge' object connecting the two theories.
As in Linguistics, literal-type translations between mathematical theories are rarely very interesting, since they do not transform a result written in the language of one theory into a substantially different result written in the language of the other theory and therefore one cannot reasonably expect that if a problem is particularly hard in the context of one theory its translation in the context of the other theory will be significantly easier to solve. The striking fact is that, unlike in Linguistics, in Mathematics, thanks to the 'bridging' role that the notion of classifying topos can play between distinct mathematical theories sharing a common semantics (technically speaking, Morita-equivalent theories), we now dispose of a set of systematic techniques for performing 'good translations' between different theories, translations which can actually change the shape and level of 'mathematical depth' of a problem in a very substantial way.
In fact, the classifying topos of a theory is a 'concrete' object which condenses in itself the semantics of the theory and can be used as a 'bridge' for transferring information to any other theory classified by it, in the sense that several different invariant properties can be defined on the classifying topos and expressed, by using the representation theory of toposes, in terms of properties of the two theories. The translations performed with this method are in general highly non-trivial, but at the same time practically feasible (and even mechanizable in many cases) due to the fact that the representation theory of toposes, on which they are based, is a technically deep but tractable subject.
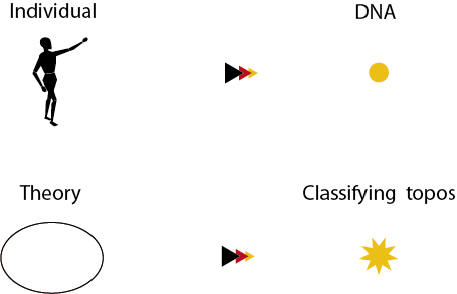
An analogy with Genetics: the classifying topos as a sort of DNA
The kind of insight that topos-theoretic methods can bring into Mathematics is comparable to that which Genetics is bringing into Medicine (apologies to biologists for any inaccuracies about their subject that may show through the rest of this section).
As the (human) DNA embodies the essential features of an individual, so the classifying topos embodies the essential features of a mathematical theory.
As the DNA can be extracted in many different ways (for example, from different parts of an individual), so the classifying topos can represented and calculated in alternative ways (emphasizing distinct readings of the core of a theory).
As the DNA is invariant with respect to the particular physical appearance of the individual at a given time (for example, with respect to age), so the classifying topos is invariant with respect to particular presentations of the theory (for example, with respect to a particular axiomatization of it over its signature).
As the DNA of an individual can be studied by using appropriate techniques, which are not those of traditional Medicine, so classifying toposes can be studied by using peculiar methods (i.e. those of Topos Theory) which, although being entirely mathematical, differ from those of classical Mathematics.
As in Genetics one studies how modifications of the DNA influence the characteristics of an individual, similarly in Topos Theory one can study the effect that topos-theoretic operations on toposes have on the theories classified by them.
As the role of the DNA is that of a unifying concept enabling us to compare individuals with each other, point out differences and discover similarities, so the notion of classifying topos is a unifying one, enabling us to compare distinct mathematical theories with each other and transfer knowledge between them.
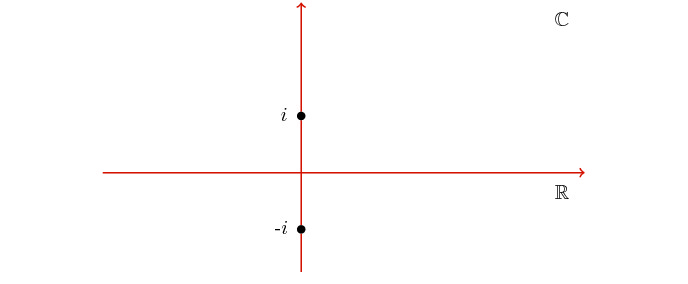
Toposes as 'natural environments' for mathematical theories
Consider the problem of classifying the solutions to polynomial equations in one variable with real coeffients. Let us in particular focus on the equation
Although a consideration of the signs of the numbers involved immediately leads to a proof of the fact that this equation does not have any solutions in the real line, the kind of understanding of this fact provided by the consideration of the same equation in the extended context of the complex plane is far more illuminating; indeed, thanks to the fact that in the complex plane roots for polynomial equations in one variable with complex (in particular, real) coefficients always exist, we are able to visualize the roots in this extended enrironment, to contemplate their symmetries and ultimately to classify them, something which is simply impossible to achieve while remaining in the original context of the real line.
The fundamental theorem of algebra, which expresses a crucial symmetry between the degree of the polynomial and the number of its roots (counted with their multiplicities) actually shows that the complex plane is a much more 'natural' environment for considering polynomial equations than the real line is. In fact, once the phenomenon is observed in this broader, symmetric, context, the 'unnaturality' of the real line as a mathematical environment for investigating this kind of problems, reveals itself very clearly.
What this story, as well as many other similar ones, 'morally' teaches us is the fact that when mathematical problems appear intricate and intractable in the context of a given 'mathematical environment', and do not exhibit significant symmetries in it, one should seriously try to construct an extension of that environment in which the problem acquires a more canonical or symmetric expression.
The 'price to pay' for achieving 'symmetry' by extending the original environment is the introduction of imaginaries, that is mathematical objects which are 'artificially' built in a purely formal way with the sole purpose of completing the given environment with respect to some kind of property or operation, and which therefore do not admit 'concrete representations' as the objects in the original environment. To say it briefly, in order to gain symmetry, one has to accept abstraction.
In the case of the example above, the original environment is the real line, while the 'imaginaries' are precisely the complex numbers. Notice that the field of complex numbers is constructed as a formal quotient
starting from the real line
.
The purpose of adding these imaginaries was to formally introduce a root to the equation
The result of this construction is a field, that of complex numbers, which does not only contain such a root, but also any other root of the same equation.
In fact, the relationship between a mathematical theory and its
classifying topos with regard to the problem of classifying the models
of the theory is comparable to that between a polynomial equation and
its splitting field (in particular, the equation
and the complex plane) with regard to the problem of classifying
the symmetries of its roots.
Considering only the set-based models of the theory, rather than all its topos-theoretic models, corresponds to restricting one's attention to the real line, as a domain of investigation in which roots should be looked for.
Extending the consideration of the models of the theory from the set-theoretic framework to the topos-theoretic one allows us to achieve a more 'symmetric' and natural environment for investigating the semantics of the theory, namely the collection of all the topos-theoretic models of the theory represented by its classifying topos.
As A. Joyal already observed in the seventies, the theory of Grothendieck toposes admits an analogy with the theory of rings, with the classifying topos of a given theory corresponding to the quotient of a polynomial ring in one variable by the ideal generated by a given polynomial (notice that the latter object classifies exactly the roots of the polynomial in arbitrary rings).
In the context of the theory of fields, the quotient of a polynomial
ring in one variable by the ideal generated by a given polynomial is not
necessarily a field, and the most natural analogue of the classifying
topos of a theory over a given topos is the splitting field
of a separable polynomial with coefficients in a given field.
Specifically, a base field
corresponds to a base topos
, the
separable extensions of
correspond to the toposes defined over
, a
separable polynomial with coefficients in
corresponds to a geometric theory over
, and
its splitting field
to its classifying topos. In fact, if we fix an order of the roots
of the polynomial
(which we assume to be of degree
and to
belong to
) we
obtain that the homomorphisms of fields over
from
to
correspond precisely to the ordered sets of roots
of 
in
which
satisfy all the polynomial relations existing between the roots of
in
,
or equivalently the n symmetric relations between them imposed by the
equality between
and
the polynomial obtained as the product of the linear factors
corresponding to its
roots; in particular, if
is a
Galois polynomial then its splitting field classifies precisely the
roots of
in
. The
models of the geometric theory attached to the polynomial can thus be
thought of as the ordered sets of roots with such property, equivalently
as the ordered sets of roots of P such that the product
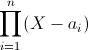of the linear polynomials associated to them is equal to P.
Polynomials with isomorphic splitting fields correspond to Morita-equivalent theories (that is, theories with equivalent classifying toposes). As in the case of toposes, this equivalence relation is highly non-trivial and identifies several syntactically different objects with each other; for example, two Galois polynomials have isomorphic splitting fields if and only if every root of the first can be expressed as a polynomial in any root of the other.
As one can characterize the finite sets of elements of a separable
extension of
which
are the set of roots of a polynomial with coefficients in
by
means of a closure condition (that is, as the sets which are stabilized
by the action of the absolute Galois group of
), so
one can naturally characterize the classes of structures inside
Grothendieck toposes which are the classes of models of a geometric
theory by means of closure conditions (cf.
this paper).
As every polynomial admits a complete set of roots in its splitting field (a set which in fact 'generates' all the other ordered sets of roots with the same property), so every geometric theory admits a model in its classifying topos (a model which in fact 'generates' all the other models of the theory).
As the symmetries of the roots of a polynomial are best investigated in the context of its splitting field (by Galois theory), so the models of a mathematical theory are best understood from the point of view of the classifying topos of the theory.
As the theory of separable field extensions of a given field is closed under the operation of taking the 'splitting field' of a given separable polynomial with coefficients in the field, so the theory of Grothendieck toposes is closed under the operation of taking 'classifying toposes' of geometric theories defined over a given topos.
Photographs from a plane: the importance of a natural point of view
As argued above, classifying toposes provide a natural, symmetric, environment for investigating the semantics of geometric theories. In fact, they do not only represent the ideal context for investigating the semantics of a theory in itself, but also provide an effective point of view from which to observe the relationships between the given theory and other mathematical theories written in different languages.
In general, the identification of the 'right point of view' to adopt on a given problem may well be a prelude for its correct solution. A convenient point of view (relatively to a given problem) is one which illuminates the essential aspects of the problem as well as their interrelations. Very often in Mathematics, in order to compare with each other two different objects belonging to a certain subfield, one constructs, separately from each of them but by following the same abstract transformative rule, two other objects of different nature, possibly belonging to a different subfield of Mathematics; then one proceeds to compare these two new objects with each other by employing methods of the latter field, being confident that such a comparison will shed light on the two original objects by virtue of the relationships which subsists between each of them and their images under the 'transformative rule'. Usually one requires the transformation rule to be invariant, that is to preserve the criterion of identity present in the original category to which the two objects belong. For example, the fundamental group is an algebraic invariant of topological spaces.
Now, the majority of invariants in Mathematics allow to compare with each other objects belonging to a certain subfield, but not arising in the context of possibly completely different areas. On the other hand, the notion of classifying topos, due to its level of generality, allows to compare mathematical theories of essentially any kind with each other, thus paving the way for establishing powerful connections between distinct fields.
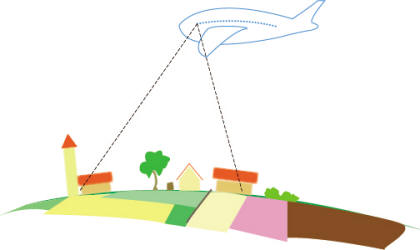
We can informally describe the relationship that a topos bears to classical Mathematics as analogous to that which a plane flying at a moderate height bears to the Earth. In fact, the level of generality of a (meta-mathematical) concept with respect to Mathematics can be compared to the height over the sea at which a plane flies. Incidentally, our view of toposes in the context of the unification project is that of meta-mathematical concepts (rather than purely mathematical ones) which can shed light on Mathematics as a whole.
As a plane flying at a certain height provides a view of a variety of different places on the Earth, so a meta-mathematical concept gives a perspective on a variety of specific mathematical objects.
The higher is the height of a plane, the larger is the portion of territory that we can expect to be able to observe from it, but the smaller is the amount of detail about the single places that such outlooks can contain. Similarly, the higher is the level of generality of a concept, the larger is the amount of different concepts which it can subsume, but the lower is the level of mathematical depth of the insights on them which it can generate.
The choice of an ideal height for shedding light on a given phenomenon is thus a crucial but non-trivial matter: the higher is not always the better. For example, the level of generality of elementary toposes, unlike that of Grothendieck toposes, is too high to be able to generate by itself non-trivial results into distinct mathematical fields; in fact, due to their lack of sites of definition, elementary toposes, as well as categories, can essentially allow only a static unification rather than a dynamic unification.
As it is important, given a set of concrete places on the Earth, to identify a convenient height at which a plane should fly in order for one to be able to see all of them in a single outlook, so it is important in Mathematics, given a set of different mathematical objects, to find a unifying concept which subsumes all of them (cf. static unification) or which allows to compare them with each other possibly allowing a transfer of information between them (cf. dynamic unification).
It is impossible, or at least extremely difficult, to compare two places which are geographically distant from each other by remaining at the level where they lie, that is on the Earth. Certainly, by staying on the Earth one can get a more detailed understanding of each of the two places separately, but not a unified view of them, that is a good perspective on their mutual relationships.
It is only by elevating oneself to a certain height, as it can be achieved for instance by flying on a plane, that one is able to embrace the two different places in a single outlook, and hence effectively compare them with each other.
The importance of the 'right' point of view, both in Mathematics and in other subjects, cannot be overstated. Things which are invisible or extremely hard to see from a certain point of view can become completely clear and natural from another. Thus the apparently innocuous choice of changing the point of view can have indeed, by itself, crucial consequences (think for example of the Copernican revolution - cf. the analogy with astronomy).
A good point of view is one which allows to obtain illuminating images of the specific context which one wants to investigate. To adopt a 'good' point of view is important both because images usually contain in themselves a great amount of information which can be extracted in a systematic way by using a variety of different tools, and because images provide a visual understanding of a phenomenon, a kind of understanding which is much more naturally appealing to the human mind than a formal series of logical steps.
The images that one can obtain by looking at Mathematics from a topos-theoretic viewpoint can be compared to the photographs of the Earth that one can shoot while flying on a plane at a moderate height on it.
Specifically, two theories connected by a topos-theoretic 'bridge' correspond to different places on the Earth to be observed from a plane. The Morita-equivalence between them provides the concrete position of the plane in the air, while the different invariants and site characterizations for their common classifying topos correspond to the different angles from which one can shoot a photograph.
In fact, every result generated through this method can be seen as a 'photograph' of the relationships between the two theories shot from the given Morita-equivalence. This is why it is so easy and natural, and even automatic in many cases, to generate results through the 'bridge-building' method; technique apart, it is just as simple as shooting a series of photographs from a plane.
Reality as a unifying concept: 'bridges' between perceptions
What is reality? Reality is usually defined as what exists in an absolute sense, that is independently from the perceptions of any particular subject or 'observer'.
Why should we suppose the existence of a (unique) reality? The most compelling reason for doing so is probably the fact that we have a continued and repeated experience in our life of coherence relations existing between the perceptions (meaning the images which come to our consciousness) of different individuals or measuring instruments (mediated by our own perception of them, a perception from which, as a matter of fact, we cannot escape). The 'realist hypothesis' (that is, the hypothesis of the existence of a unique reality) provides a natural intuitive explanation for such a phenomenon (in fact, arguably the simplest of all the possible explanations), based on the idea that reality could play the role of a unifying entity among the different perceptions, an entity which can moreover be considered ontologically 'responsible' for the existence of the individual or 'mechanical' (and then individually mediated) perceptions.
Under the realist hypothesis, which in fact is widely accepted, we thus have two levels: that of reality and that of perceptions, or, in other words, that of objectivity and that of subjectivity. The investigation of the nature of the relationships between the two levels is the formal subject of study of phenomenology, but the fundamental character of such problem makes it of course relevant for essentially any kind of intellectual endeavor.
We can thus consider sensibly real whatever is invariant with respect to perceptions. Such a remark clearly presupposes the existence of a criterion of identity for perceptions, which allows to discriminate when two perceptions can be considered the same or not. Anyway, whatever such a criterion might be, the manifestation of reality can be identified with the collection of all perceptions, modulo a certain equivalence relation, namely the relation corresponding to such criterion of identity. The identity criterion between perceptions should precisely formalize the 'coherence relations' existing between them which we mentioned above, so that such relations become identities in the resulting quotient, that is at the level of (sensible) reality.
The different perceptions can thus be seen as different manifestations of the unique reality in the context of different 'observers', and reality acts as a unifying 'bridge' between the observers, relating each of them to one another by virtue of the coherence relations existing between their individual perceptions.
Notice that any perception of a given 'observer' is entirely and canonically determined by the characteristics of the observer and its position in space-time. In other words, individuals (or measuring instruments) are canonical 'generators' of perceptions, perceptions that can then be compared with each other according to the particular criteria of identity that one chooses.
Sensible reality, as defined in this way, thus captures the true essence of perceptions, representing the aspects of things which do not depend on their different 'projections' in the direction of individual observers.
A familiar, platonic, image that comes to mind in thinking about this is that of a sun which 'generates' different shadows in the direction of the concrete forms of matter on which it impacts. In fact, as the sun is a unifying source of shadows, so reality is a unifying source of perceptions. As shadows are easily comparable with each other only if one bears in mind that they ultimately come from a unique source, so the coherence relations existing between the perceptions of different observers are hard to explain without invoking the existence of a unique reality, an assumption which in fact constitutes the main foundation of Science.
The analogue of these concepts in the topos-theoretic context is the following. Individual observers correspond to Morita-equivalent theories, reality to their classifying topos and the specific characteristics of the observers in space-time to the different sites of definition of the classifying topos.
In fact, as reality acts as a 'bridge' for relating different individuals to each other, so a topos can act as a 'bridge' for transferring information between the different theories classified by it.
Bridges in Finance: trading through stock 'bridging'
The subject of technical analysis of stock markets is based on the assumption that the behavior of stock markets is, although highly impredictable, not completely casual. There are 'invariants' of stocks which can be seeked and profitably exploited, once identified, to make effective investments. A good technical trading system will thus 'bridge' stocks on the basis of selected invariants which they share at different instants. In fact, a given stock at a certain time may display a similar behaviour to that of a different stock at another time. Switching from one stock to another with the aim of getting a certain property having a high likelihood of producing a positive earning preserved in the process, is thus a sensible strategy which, provided that the properties which are supposed to remain invariant across the market evolutions are well-chosen, can lead to significant earnings.
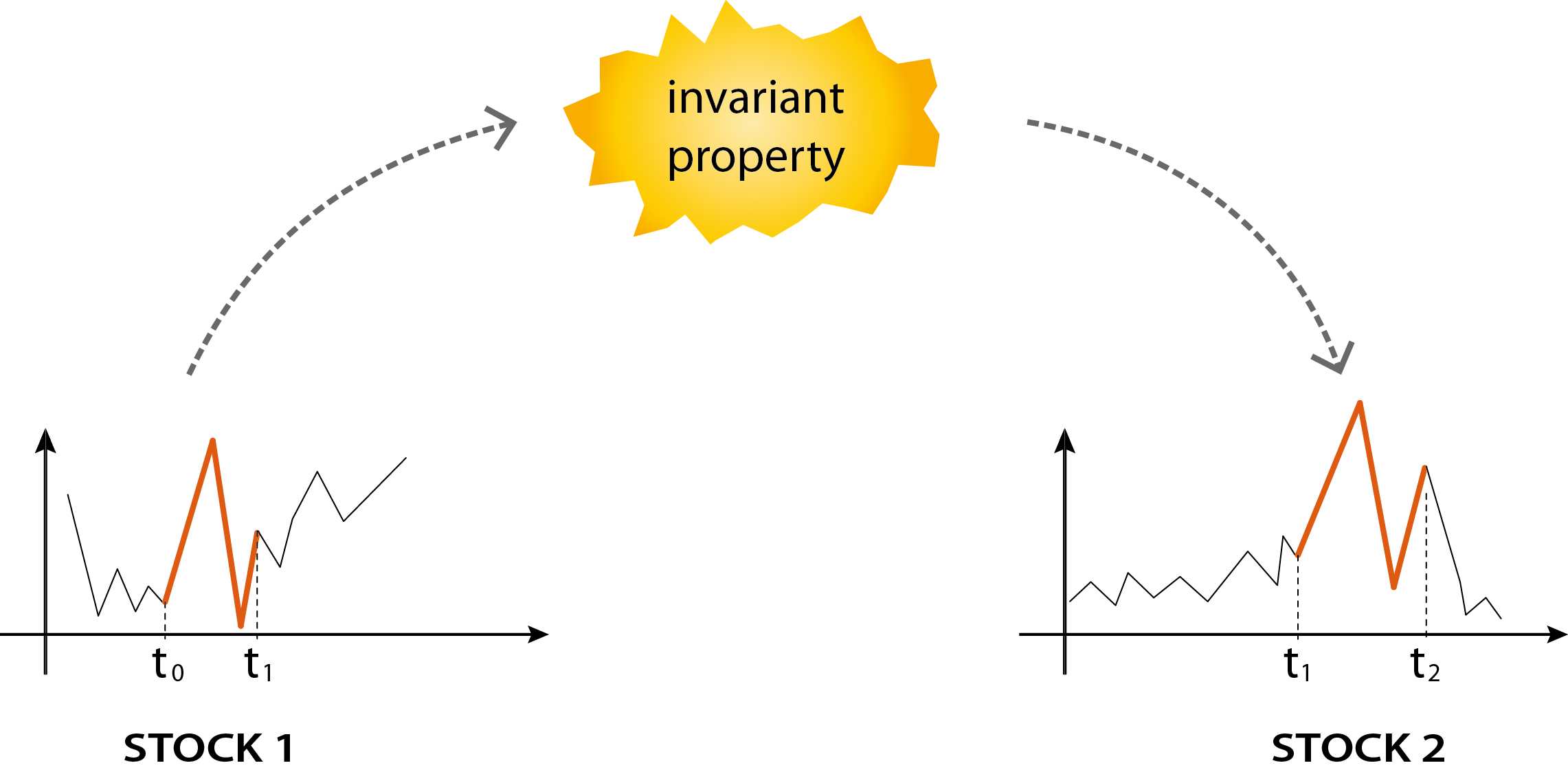
In a trading system based on the principles illustrated above, it is the invariants, rather than the stocks, which guide the investments. Most of these invariants of stocks are not visible to the naked eye, nor easily quantifiable without a technical frame of reference. On the other hand, once appropriately formalized in mathematical language and implemented in a computer program, such properties can be effectively and systematically researched throughout the whole apparently chaotic universe of stock markets.
Of course, the main difficulty lies in choosing relevant invariants and predicting with enough precision when a certain stock will realize a particular selected invariant. For achieving this, a systematic analysis by a computer of the past history of stocks in view of the current circumstances of the market turns out to be an essential and decisive tool.
In relation to the view 'toposes as bridges', the equivalent of a site in this context is a pair consisting of a stock and an instant at which it is considered, while the equivalent of a topos-theoretic invariant is some crucial property which the trading system tries to keep invariant across the buy/sell operations of switch between stocks which it performes.
This trading philosophy has been implemented by an Italian software company, namely EOS S.r.l., which has realized, following my advice and under the leadership of my father, a stock trading system, Up-Down Forecast, used by the investment company Cellino e Associati SIM S.p.A., which obtained the prize “Tripla A” of Milano Finanza as the most successful stock investment line in Italy in 2015 with a +37.70% of earnings and a differential of +22.30% with respect to the benchmark (see here).
We thank Giorgio Veglia for kindly realizing the pictures reported in this page.