Olivia Caramello's website
Unifying theory
Toposes as 'bridges'
General overview
![]() one
can canonically associate a site such that the topos built from it can
be identified with its classifying topos
one
can canonically associate a site such that the topos built from it can
be identified with its classifying topos
![]() .
.
The basic idea underlying the unification methodologies is that the classifying topos
![]() of a
theory
of a
theory ![]() can be effectively used as a 'bridge' to transfer information between the theory
can be effectively used as a 'bridge' to transfer information between the theory
![]() and any other theory
and any other theory
![]() which is Morita-equivalent to it:
which is Morita-equivalent to it:
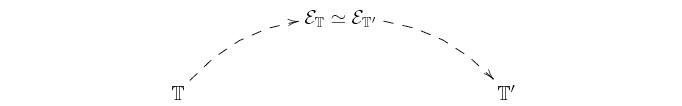
T
The unifying methodologies
The fundamental intuition underlying the unifying methodologies is that a given mathematical property can manifest itself in several different forms in the context of mathematical theories which have a common semantics but a different linguistic presentation.
A (Grothendieck) topos can be thought of as a mathematical object which condenses in itself the semantics of a mathematical theory, representing the body of properties of the theory which do not depend on its linguistic presentation but only on its semantics. To any mathematical theory (of a general specified form) one can associate a topos, canonically built from any presentation of it, which represents its 'semantical core'. Such an object is called the classifying topos of the theory.
Two mathematical theories have the same classifying topos (up to equivalence) if and only if they have the same 'semantical core', that is if and only if they are indistinguishable from a semantic point of view; such theories are said to be Morita-equivalent. Conversely, every Grothendieck topos arises as the classifying topos of some theory.
Many important dualities and equivalences in Mathematics can be naturally interpreted in terms of equivalences between the classifying toposes of different theories; on the other hand, Topos Theory itself is a primary source of Morita-equivalences. It is fair to say that the notion of Morita-equivalence formalizes in many situations the feeling of 'looking at the same thing in different ways', and in fact it is ubiquitous in Mathematics.
Now, Grothendieck toposes can serve as 'bridges' for transferring
information between Morita-equivalent theories in the following sense. The existence of different presentations for the
'semantical core' of a given mathematical theory translates, at the technical level, into the existence of different representations (technically speaking,
sites) for the classifying topos of the theory.
Topos-theoretic invariants, that is properties of toposes or constructions on them which are invariant under equivalence, can then be used to transfer properties between the two representations of the classifying topos and hence between the two theories. The transfer of properties arises from the process of expressing properties of toposes in terms of properties of their representations: these relationships between properties of sites
![]() and properties of toposes
and properties of toposes
![]() are called
site characterizations.
are called
site characterizations.
Given a Morita-equivalence and a topos-theoretic invariant I, site characterizations for I play in this context the role of the 'arches' of the bridge, the 'deck' of the bridge being given by the equivalence of toposes expressing the Morita-equivalence. The topos-theoretic invariant I thus acts in this context as a tool enabling to bring certain information from one side of it to the other of the equivalence; different invariants allow us to transfer different information.
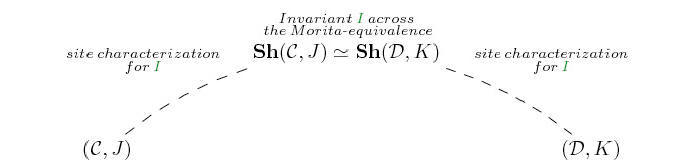
This methodology is very effective from a
technical viewpoint due to the fact that the relationship between a site
![]() and the
topos
and the
topos ![]() which it generates is technically very well-behaved (although highly
non-trivial), to the extent that for many important classes of
invariants there exist natural bijective site characterizations holding
uniformly for any site, or at least for large classes of them. Also,
there exist infinitely many topos-theoretic invariants (and one can
always easily introduce new ones - since, by an obvious metatheorem, any
property written in the language of Topos Theory is automatically
invariant with
respect to the notion of equivalence of toposes, namely categorical
equivalence - and seek natural site characterizations for them).
which it generates is technically very well-behaved (although highly
non-trivial), to the extent that for many important classes of
invariants there exist natural bijective site characterizations holding
uniformly for any site, or at least for large classes of them. Also,
there exist infinitely many topos-theoretic invariants (and one can
always easily introduce new ones - since, by an obvious metatheorem, any
property written in the language of Topos Theory is automatically
invariant with
respect to the notion of equivalence of toposes, namely categorical
equivalence - and seek natural site characterizations for them).
We can thus think of a topos as an object which, together with all its different representations, embodies in itself a great amount of relationships existing between the different theories classified by it. Any topos-theoretic invariant thus behaves like a 'pair of glasses' which allows to discern certain information which is 'hidden' in a given Morita-equivalence.
These methods unify distinct mathematical theories with each other in the sense that properties (resp. constructions) arising in the context of theories which have a common 'semantical core' but a different 'linguistic presentation' come to be seen as different manifestations of a unique property (resp. construction) lying at the topos-theoretic level.
As a matter of fact, these methodologies define a novel way of doing Mathematics which is inherently 'upside-down' with respect to the more traditional approaches in which one starts with simple ingredients and proceeds to combine them to build more complicated structures. Indeed, these methodologies take as primitive ingredients rich and sophisticated mathematical entities, namely Morita-equivalences and topos-theoretic invariants, and allow one to extract from them a huge amount of information relevant for classical mathematics (it should however be noted that the fact that these 'primitive ingredients' are intrinsically complex does not imply that it is difficult to obtain such objects from the current mathematical practice, as it can be seen from my papers).
This intrinsically 'top-down' approach is actually liable to generate a great number of surprising insights into a variety of different mathematical contexts, a sort of uniform 'rain of results' into distinct subfields, results which could well be hard to establish, or even to merely imagine, by using the specialized methods of the different fields. As in the case of rain it is difficult, if not impossible, to predict where any single drop of it will fall, so in the case of the unifying methodologies it is hard to predict with certainty and exactness which results will be generated by the abstract machinery; on the other hand, as the power of the rain lies in the energy and matter which it globally generates, as well as in its uniform nature, so the power of the unifying methodologies lies in their 'global fruitfulness' and 'uniform' ramifications spreading transversally across the various subfields of Mathematics.
In fact, the creative power of these methodologies, as well as their uniform and canonical nature, makes them effective tools for assisting specialists of the various domain in the discovery of specific results, as well as a concrete guide for developing mathematics in a cohesive and conceptually inspired way.
Incidentally, it should be noted that these methodologies could also be generalized to the case of 'bridges' whose deck is given by some kind of relationship between toposes which is not necessarily an equivalence, in the presence of properties or constructions of toposes which are invariant with respect to such a relation. Nonetheless, the advantage of focusing on Morita-equivalences is twofold; from a technical vewipoint, it is convenient because all natural topos-theoretic properties that one can formulate are automatically invariant with respect to categorical equivalence of toposes, while from a conceptual viewpoint it can be naturally interpreted as a unifying technique, since the properties of the different theories come to be interpreted as different manifestations of a unique property lying at the topos-theoretic level.
The unifying methodologies are also effective from a computational viewpoint. Indeed, the well-behaved representation theory of Grothendieck toposes allows to translate properties and results between different theories in a uniform and 'semi-automatic way'. In particular, one can generate a great number of non-trivial insights in different mathematical fields without really making any real creative effort. Of course, not all of the results generated in this way are necessarily 'interesting mathematical theorems'; many of them can be rather 'weird' according to usual mathematical standards, and in fact, in order to get interesting results, one has to use one's mathematical sensitivity to 'programme the machine' appropriately (that is, by choosing topos-theoretic invariants and Morita-equivalences in a sensible way); but these results can still be quite deep, due to the non-trivial nature of the representation theory of Grothendieck toposes.
Toposes can thus act as 'universal translators' across different mathematical theories in a very effective and fruitful way. From a technical point of view, the main reason for this effectiveness is two-fold: on one hand, topos-theoretic invariants usually manifest themselves in significantly different ways in the context of different sites (think for example of the amalgamation property on a category or the property of a topological space to be extremally disconnected, which represent different manifestations of a given topos-theoretic invariants, namely the property of a topos to satisfy De Morgan's law, in the context of different sites - see here for more details), while on the other hand the site characterizations for them which formally express such manifestations are essentially canonical and can be generally established in a systematic, and in many cases even mechanical, way, due to the very well-behaved nature of the representation theory of Grothendieck toposes in terms of sites.
Concerning the level of 'mathematical depth' of the translations established through the bridge technique, we remark that it is clearly impossible to accurately predict it a priori. Anyway, an upper bound for the complexity of such results is given by the sum of the mathematical depth of the three parts of the bridge, namely its 'deck' (given by the Morita-equivalence) and its two 'arches' (given by the site characterizations), which nonetheless can be very considerable (due to the depth of topos-theoretic methods).
Actually, while in most cases the topos-theoretic translations do not admit easy or natural elementary proofs, it may happen that, after discovering a certain 'translation' through the bridge method, one could find a 'concrete' proof of it which does not involve toposes; but even in these cases one often realizes that, in spite of its greater technical complexity, it is the topos-theoretic proof that best illuminates the 'real reason' why the result is true, and also that ultimately it would have been rather hard, if not impossible, to arrive at the result or even imagine it without the 'guide' of toposes. Indeed, the topos-theoretic proofs arising from applications of the bridge method are natural both from a technical viewpoint (because of their canonicity) and from a conceptual one (because of their unifying nature, which reveals itself in the fact that the method relates to each other properties (or constructions) which represent different concrete manifestations of a unique abstract property (or construction) lying at a higher level.
In a sense, the 'upside-down' way in which the results are generated through the bridge method is so different from the traditional techniques that it defines by itself a new way of doing Mathematics, intrinsically intra-disciplinary in character, which owes its strength to the identification of 'centres of mathematical symmetry' from which mathematical reality can be naturally observed. In fact, the naturality of this point of view is witnessed by its technical fruitfulness and creative power, which reflects itself in the possibility of a 'canonical' and computationally effective generation of concrete applications in distinct mathematical domains.